Question

An Australian emu is running due north in a straight line at a speed of 13.0 m/s and slows down to a speed of 10.5 m/s in 4.20 s. (a) What is the magnitude and direction of the bird’s acceleration? (b) Assuming that the acceleration remains the same, what is the bird’s velocity after an additional 1.50 s has elapsed?

Answer 1

Step-by-step explanation:

It is given that,

Initial velocity of the bird, u = 13 m/s

Final speed of the bird, v = 10.5 m/s

Time taken, t = 4.20 s

(a) Acceleration of the bird is given by :

`a=(v-u)/(t)`

`a=(10.5\ m/s-13\ m/s)/(4.20\ s)`

`a=-0.59\ m/s^2`

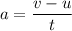
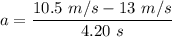
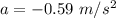
So, The direction of acceleration is opposite to the direction of motion.

(b) We need to find the bird’s velocity after an additional 1.50 s has elapsed i.e. t = 4.2 + 1.5 = 5.7 s. Let v' is the new final velocity.

It can be calculated using first equation of motion as :

`a=(v'-u)/(t)`

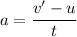
v' = u + at

`v'=(-0.59)* 5.7+13`

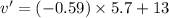
v' = 9.64 m/s

Hence, this is the required solution.