Question

the graph of y= sqrtx is translated 4 units left and 1 unit up to create the function h(x). the graph of h(x) is shown on the coordinate grid. what is the range of h(x)?

Answer 1

The range of the function h(x) is
`R=\y`

Explanation:

Given : The graph of
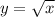`y=√(x)` is translated 4 units left and 1 unit up to create the function h(x).

To find : What is the range of h(x)?

Solution :

When the graph f(x) is translated then

1) f(x)+b shifts the function b units upward.

2) f(x + b) shifts the function b units to the left.

The graph of
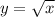`y=√(x)` is translated 4 units left.

i.e.
`y=√(x+4)`

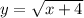
The graph of
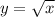`y=√(x)` is translated 1 unit up.

i.e.
`y=√(x+4)+1`

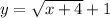
So, The required function h(x) is
`h(x)=√(x+4)+1`

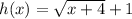
The range of a function is set of output values produce by a function.

In the given graph, y value is always greater than and equal to 1.

So, The range of the function h(x) is
`R=\y\geq 1\`

Answer 2

C.
`\y\ge 1\.`

Explanation:

Consider the parent function
`f(x)=√(x).`

• The domain of this function is
  `x\ge 0;`
• The range of this function is
  `y\ge 0.`

Now consider given function
`h(x)=√(x+4)+1` (translated 4 units left and 1 unit up.)

• The domain of this function is
  `x\ge -4;`
• The range of this function is
  `y\ge 1.`