Question

What is the surface area of the cone? (Use 3.14 for pi .)

794.42 in.2
483.56 in.2
822.68 in.2
414.48 in.2

Answer 1

794.42 in² (since I used the pi = 3.14159 , the result is slightly different,

Explanation:

Formula: Given radius and slant height calculate the height, volume, lateral surface area and total surface area.

Given r, s find h, V, L, A

h = √(s² - r²)

r = 11 in

h = 4.796 in

s = 12 in

V = 607.7 in³

L = 414.7 in²

B = 380.1 in²

A = 794.8 in

Agenda: r = radius

h = height

s = slant height

V = volume

L = lateral surface area

B = base surface area

A = total surface area

π = pi = 3.14159

√ = square root

Answer 2

Answer: the correct option is

(A) 794.42 in.²

Step-by-step explanation: We are given to find the surface area of the cone shown in the figure.

We know that

the SURFACE AREA of a cone with height h units and radius r units is given by

`S=\pi r(r+√(h^2+r^2)).`

For the given cone, we have

r = 11 in. and

`h=√(12^2-11^2)=√(144-121)=√(23)=4.8.`

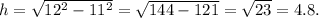
Therefore, the surface area of the given cone is

`S\\\\=\pi r(r+√(h^2+r^2))\\\\=3.14*11(11+√(4.8^2+11^2))\\\\=34.54(11+12)\\\\=34.54*23\\\\=794.42.`

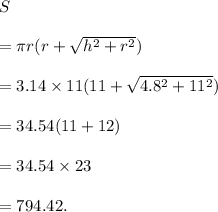
Thus, the required surface area of the given cone is 794.42 in.²

Option (A) is CORRECT.