Question

Recipe ingredients remain in a constant ratio no matter how many servings are prepared. Which table shows a possible

ratio table for ingredients X and Y for the given number of servings?

Answer 1

The correct option is 4.

Explanation:

It given that recipe ingredients remain in a constant ratio no matter how many servings are prepared.

It means the relation between x and y is

`y\propto x`

`y=kx`

where k is constant of proportionality.

We need to find a possible ratio table for ingredients X and Y for the given number of servings.

In table 1,

`(y_1)/(x_1)=(2)/(1)`

`(y_2)/(x_2)=(3)/(2)`

`(y_1)/(x_1)\\eq (y_2)/(x_2)`

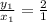
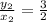
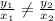
Option 1 is incorrect.

In table 2,

`(y_1)/(x_1)=(2)/(1)=2`

`(y_2)/(x_2)=(4)/(2)=2`

`(y_3)/(x_3)=(8)/(3)`

`(y_1)/(x_1)\\eq (y_3)/(x_3)`

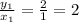
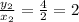
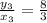
Option 2 is incorrect.

In table 3,

`(y_1)/(x_1)=(2)/(1)`

`(y_2)/(x_2)=(3)/(2)`

`(y_1)/(x_1)\\eq (y_2)/(x_2)`

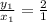
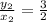
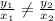
Option 3 is incorrect.

In table 4,

`(y_1)/(x_1)=(2)/(1)=2`

`(y_2)/(x_2)=(4)/(2)=2`

`(y_3)/(x_3)=(6)/(3)=2`

`(y_)/(x_1)=(y_2)/(x_2)=(y_3)/(x_3)`

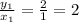
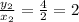
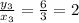
Option 4 shows a possible ratio table for ingredients X and Y for the given number of servings.

Therefore the correct option is 4.

Answer 2

Table N 4

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
`y/x=k` or
`y=kx`

Verify the table 4

For x=1, y=2

so

y/x=2/1=2

For x=2, y=4

so

y/x=4/2=2

For x=3, y=6

so

y/x=6/3=2

therefore

The constant of proportionality k is equal to 2 and the equation is equal to

y=2x

The table 4 represent a direct variation, therefore is a possible ratio table for ingredients X and Y