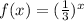Question

Consider the exponential function f(x)
its
graph.​

Answer 1

# The growth value of the function is 1/3 ⇒ 2nd

# f(x) shows exponential decay ⇒ 3rd

# The function is a stretched of the function
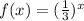`f(x)=((1)/(3)) ^(x)` ⇒ 4th

Explanation:

* Lets explain the exponential function

- The form of the exponential function is f(x) = a b^x, where a ≠ 0,

b > 0 , b ≠ 1, and x is any real number

- a is the initial value of f(x) ⇒ (when x = 0)

- b is the growth factor

- The exponent is x

- If the growth factor (b) is in between 1 and 0 then it is exponential

decay

* Lets solve the problem

∵
`f(x)=3((1)/(3))^(x)`

- Lets find the initial value

∵ At the initial position x = 0

∴
`f(0)=3((1)/(3))^(0)=3(1)=3`

* The initial of f(x) is 3

∵ b = 1/3

∵ b is the growth factor of the function

* The growth value of the function is 1/3

∵ b = 1/3

∵ 0 < b < 1

∴ The function is exponential decay

* f(x) shows exponential decay

- A vertical stretching is the stretching of the graph away from the x-axis

- If k > 1, the graph of y = k•f(x) is the graph of f(x) vertically stretched

∵
`f(x)=((1)/(3))^(x)`

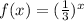
∵ Its parent function is
`f(x)=3((1)/(3))^(x)`

∴ k = 3

∵ k > 1

∴ the function is stretched vertically

* The function is a stretched of the function
`f(x)=((1)/(3))^(x)`

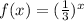
∴ The true statements are:

# The growth value of the function is 1/3

# f(x) shows exponential decay

# The function is a stretched of the function
`f(x)=((1)/(3))^(x)`