Answer:
d = 15 mm
Step-by-step explanation:
Force of repulsion between two current carrying wire is given by
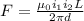
now this force of repulsion is counterbalanced by the weight of the wire
so we have
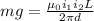
now we have

so here we can say that
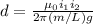
now plug in all values in it
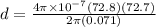
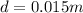
d = 15 mm