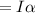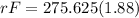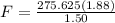Answer:
F = 345.45 N
Step-by-step explanation:
Angular acceleration of the disc is given as rate of change in angular speed
it is given by formula
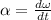
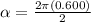
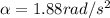
now we know that moment of inertia of the solid uniform disc is given as
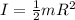


now we have an equation for torque as