Question

A stereo system is being installed in a room with a rectangular floor measuring 14 feet by 9 feet and a 7- foot ceiling. The stereo amplifier is on the floor in one corner of the room. A speaker is at the ceiling in the opposite corner of the room. What is the shortest connection

Answer 1

Approximately 24 feet.

Explanation:

Refer to the two diagrams attached (created with Geogebra.)

The wire between the speaker and the amplifier shall be routed along the wall. The length of the connection depends on the height of the point P at which the wire turns. Point P is shown in green in both diagrams.

To find the optimal position of that turning point, imagine that the two adjacent walls of the room are unfolded into two rectangles in the same plane (diagram 2.) Consider the claim: the shortest connection shall be a straight line that links the two devices when the two walls are unfolded. This explanation will show why this claim is true using the triangle inequality theorem.

Assume this claim is false: the connection will be even shorter if the wire turns at P', which is a point other than P. The length of the connection is now the sum of the two segments:

• the distance between the amplifier and P', and
• the distance between P' and the speaker.

In contrast, if the wire is routed through point P, the length of the connection will simply be

• the length of the segment between the amplifier and the speaker.

Point P is on the line that connects the amplifier and the speaker in diagram 2. However, P' is a point other than P, meaning that P' is off the line between the speaker and the amplifier. It is thus possible for the following three points to form a triangle:

• The amplifier,
• The speaker, and
• Point P'.

By the triangle inequality theorem, the sum of any two sides of a triangle is greater than the length of the third side. To make full use of this theorem, consider the length of the three sides in this triangle:

`\left\{\begin{array}{ll}\left.\begin{aligned}&\text{distance between amplifier and P}'\text{.}\\&\text{distance between P}' \text{ and speaker.}\end{aligned}\right\}&\text{Length of the second connection}\\\text{distance between amplifier and speaker}\end{array}\right.`.

The sum of the first two distances shall be greater than the third. In other words, the length of the connection through P' will be greater than the length of the connection through P. This fact contradicts the assumption that the original claim is false. In other words, the claim that P gives the shortest connection is true.

Find the length of the shortest connection using the Pythagorean Theorem. Refer to the second diagram, the connection is the hypotenuse of a right triangle with

• a leg of length
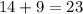  `14 + 9 = 23` feet, and
• another leg of length
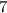  `7` feet.

The length of the connection (the hypotenuse) will be:

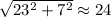`\sqrt{23^(2) + 7^(2)}\approx 24` feet.