Question

The value of a collector’s item is expected to increase exponentially each year. The item is purchased for $500. After 2 years, the item is worth $551.25. Which equation represents y, the value of the item after x years?

1. y = 500(0.05)x
2. y = 500(1.05)x
3. y = 500(0.1025)x
4. y = 500(1.1025)x

Answer 1

Option 2 is correct.

Explanation:

Actual price = $500

After 2 years the worth of item is increased to = $551.25

We need to find the equation that represents y, the value of the item after x years.

According to given information the equation can be of form

`y=500(r)^x`

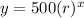
where r represents the growth and x represents the number of yeras.

We need to find the value of r that represents the growth

The value of y = 551.25, and value of x = 2

Putting values and solving:

`y=500(r)^x\\551.25 = 500(r)^2\\551.25/500 =(r)^2\\1.1025 = (r)^2\\Taking square root on both sides\\\\√(1.1025)=√((r)^2)\\  => (r) = 1.05\\`

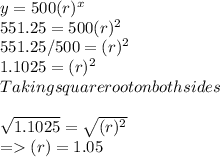
Putting value of r in the equation

`y=500(r)^x`

`y=500(1.05)^x`

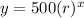
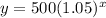
So Option 2 is correct.