Question

Which function has only one x-intercept at (-6, 0)?

Of(x) = x(x - 6)
f(x) = (x - 6)(x – 6)
f(x) = (x + 6)(x - 6)
f(x) = (x + 1)(x + 6)

Answer 1

the answer is d on edge

Explanation:

Answer 2

The function f(x) = (x - 6)(x - 6) has only one x-intercept. But at (6, 0) not at (-6, 0).

Explanation:

The intercept form of a quadratic equation (parabola):

`y=a(x-p)(x-q)`

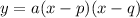
p, q - x-intercepts

Therefore

The function f(x) = x(x - 6) = (x - 0)(x - 6) has two x-intercepts at (0, 0) and (6, 0)

The function f(x) = (x - 6)(x - 6) has only one x-intercept at (6, 0)

The function f(x) = (x + 6)(x - 6) = (x - (-6))(x - 6)

has two x-intercept at (-6, 0) and (6, 0)

The function f(x) = (x + 1)(x + 6) = (x - (-1))(x - (-6))

has two x-intercepts at (-1, 0) and (-6, 0).