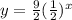Answer:
Explanation:
* Lets revise the meaning of exponential function
- The form of the exponential function is
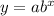 ,
,
where a ≠ 0, b > 0 , b ≠ 1, and x is any real number
- It has a constant base b
- It has a variable exponent x
- To solve an exponential equation, take the log or ln of both sides,
and solve for the variable
* Lets solve the problem
∵ y = a(b)^x is an exponential function
∵ Its graph contains the point (-4 , 72) and (-2 , 18)
- Lets substitute x and y by the coordinates of these points
# Point (-4 , 72)
∵
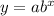
∵ x = -4 and y = 72
∴
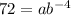
- The change any power from -ve to +ve reciprocal the base of
the power (
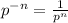
∴
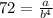
- By using cross multiplication
∴
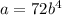 ⇒ (1)
⇒ (1)
# Point (-2 , 18)
∵ x = -2 and y = 18
∴
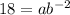
∴
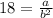
- By using cross multiplication
∴ a = 18b² ⇒ (2)
- Equate the two equations (1) and (2)
∴
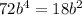
- Divide both sides by 18b²
∵
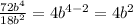
∵

∴ 4b² = 1 ⇒ divide both sides by 4
∴
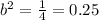 ⇒ take square root for both sides
⇒ take square root for both sides
∴ b = √0.25 = 0.5
- Lets substitute the value ob b in equation (1) or (2) to find a
∵ a = 18b²
∵ b² = 0.25
∴ a = 18(0.25) = 4.5
- Lets substitute the values of a and b in the equation
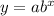
∴
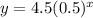
- We can write it using fraction
∴