Question

How do I solve for the minimum and maximum of the function y=-1/2x^2 -5x+2

Answer 1

Try this solution:

There are several ways to find the max or min of the given function:

1. to use derivative of the function. For more details see the attachment (3 basic steps); the coordinates of max-point are marked with green (-5; 14.5)

2. to use formulas. The given function is the standart function with common equation y=ax²+bx+c, it means the correspond formulas are (where a<0, the vertex of this function is its maximum):

`X_0=-(b)/(2a) ; \ X_0=-(-5)/(2*(-(1)/(2))) =-5.`

`Y_0=-(D)/(4a); \ Y_0=-(25+4*2*0.5)/(4*(-(1)/(2))) =14.5`

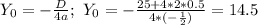
Finally: point (-5;14.5) - maximum of the given function.

3. to draw a graph.