Question

Suppose r(t) = cos t i + sin t j + 3tk represents the position of a particle on a helix, where z is the height of the particle above the ground. (a) Is the particle ever moving downward? When? (If the particle is never moving downward, enter DNE.) t = (b) When does the particle reach a point 15 units above the ground? t = (c) What is the velocity of the particle when it is 15 units above the ground? (Round each component to three decimal places.) v = (d) When it is 15 units above the ground, the particle leaves the helix and moves along the tangent line. Find parametric equations for this tangent line. (Round each component to three decimal places.)

Answer 1

The particle has position function

`\vec r(t)=\cos t\,\vec\imath+\sin t\,\vec\jmath+3t\,\vec k`

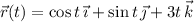
Taking the derivative gives its velocity at time
`t`:

`\vec v(t)=(\mathrm d\vec r(t))/(\mathrm dt)=-\sin t\,\vec\imath+\cos t\,\vec\jmath+3\,\vec k`

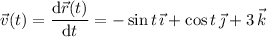
a. The particle never moves downward because its velocity in the
`z` direction is always positive, meaning it is always moving away from the origin in the upward direction. DNE

b. The particle is situated 15 units above the ground when the
`z` component of its posiiton is equal to 15:

`3t=15\implies\boxed{t=5}`

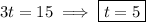
c. At this time, its velocity is

`\vec v(5)=-\sin 5\,\vec\imath+\cos5\,\vec\jmath+3\,\vec k\approx\boxed{0.959\,\vec\imath+0.284\,\vec\jmath+3\,\vec k}`

d. The tangent to
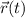`\vec r(t)` at
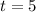`t=5` points in the same direction as
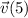`\vec v(5)`, so that the parametric equation for this new path is

`\vec r(5)+\vec v(5)t\approx\boxed{(0.284+0.959t)\,\vec\imath+(-0.959+0.284t)\,\vec\jmath+(15+3t)\,\vec k}`

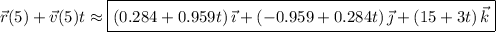
where
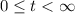`0\le t<\infty`.