Question

Are the equations lxl – 3 = 7 and [x] = 10 equivalent?

Answer 1

They're not equivalent.

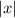`|x|` (vertical bars) represents the absolute value of x. How it works is that it turns negative numbers positive but leaves 0 and positive numbers alone (hence it gets a number's distance from 0 on the number line).

`[x]` (square brackets) usually represents the floor function, which returns the largest integer that is less than or equal to x. (The floor of x can also be written as
`\lfloor x \rfloor` --- it depends on what your textbook/source says).

To solve
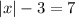`|x| - 3 = 7`, you first transform it into the equivalent equation
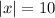`|x| = 10`. Then by definition of absolute value, there are only two solutions for the first equation: x = 10 or x = -10.

[x] = 10 has infinitely many solutions. For example, the floor of 10 is 10, so
`[10] = 10`, thus a solution for the second equation is x = 10

The floor of 10.1 is 10, so
`[10.1] = 10`, thus another solution for the second equation is x = 10.1.

The two equations do not have the same solution set (as x = 10.1 does not solve |x| - 3 = 7 but solves [x] = 10), so they're not equivalent.