Question

Solve the system of equations 4x+3y+6z=3, 5x+5y+6z=5 and 6x+3y+6z=3

Answer 1

`x=0\\y=1\\z=0`

Explanation:

Multiply the first equation by -1:

`(-1)(4x+3y+6z)=3(-1)\\\\-4x-3y-6z=-3`

Add the new equation and the third equation an solve for "x":

`\left \{ {{-4x-3y-6z=-3\ \atop {6x+3y+6z=3} \right.\\...........................\\2x=0\\x=0`

Substitute the value of "x" into the first equation and solve for "y":

`4(0)+3y+6z=3\\\\3y=3-6z\\\\y=(3-6z)/(3)\\\\y=1-2z`

Substitute the value of "x" and
`y=1-2z` into the second equation and solve for "z":

`5(0)+5(1-2z)+6z=5\\\\5-10z+6z=5\\\\-4z=0\\\\z=0`

Knowing the values of "x" and "z", you can substitute them into any original equation and solve for "y". Then:

`4(0)+3y+6(0)=3\\\\3y=3\\\\y=(3)/(3)\\\\y=1`

Answer 2

Hello!

The answer is:

The solutions to the system of equations are:

`x=0\\y=1\\z=0`

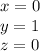
Why?

To solve the system of equations by the easiest way, we need to use the reduction method. The reduction method consist of reducing the variables applying different math operations in order to be able to isolate the variables.

So, we are given the system:

`4x+3y+6z=3\\5x+5y+6z=5\\6x+3y+6z=3`

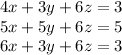
Let's work with the first and the third equation:

`4x+3y+6z=3\\6x+3y+6z=3`

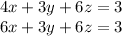
Then, multiplying the first equation by -1, we have:

`-4x-3y-6z=-3\\6x+3y+6z=3`

`-4x+6x-3y+3y-6z+6z=-3+3`

`2x=0`

`x=0`

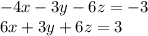
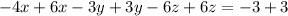
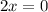
Now, working with the first and the second equation, we have:

`4x+3y+6z=3\\5x+5y+6z=5`

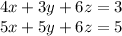
Then, multiplying the first equation by -1, we have:

`-4x-3y-6z=-3\\5x+5y+6z=5`

`5x-4x+5y-3y-6z+6z=-3+5`

`x+2y=2`

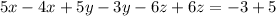
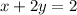
Then, substituting "x" into the equation, we have:

`0+2y=2`

`y=(2)/(2)=1`

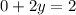
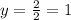
Finally, working with the first equation and substituting "x" and "y", we have:

`4x+3y+6z=3`

`4*0+3*1+6z=3`

`0+3+6z=3`

`6z=3-3=0`

`6z=0`

`z=(0)/(6)=0`

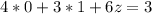
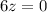
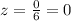
Hence, we have that the solutions to the system of equations are:

`x=0\\y=1\\z=0`

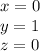
Have a nice day!