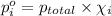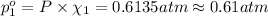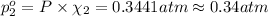Question

A gas mixture contains 1.20 g N2 and 0.77 g O2 in a 1.65-L container at 15 ∘C. Part A Calculate the mole fraction of N2. Express your answer using two significant figures. X1 X 1 = nothing Request Answer Part B Calculate the mole fraction of O2. Express your answer using two significant figures. X2 X 2 = nothing Request Answer Part C Calculate the partial pressure of N2. Express your answer using two significant figures. P1 P 1 = nothing atm Request Answer Part D Calculate the partial pressure of O2. Express your answer using two significant figures. P2 P 2 = nothing atm Request Answer Provide Feedback

Answer 1

Step-by-step explanation:

Moles of nitrogen gas =
`n_1=(1.20 g)/(28 g/mol)=0.0428 mol`

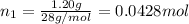
Moles of oxygen gas =
`n_2=(0.77 g)/(32 g/mol)=0.0240 mol`

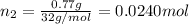
Mole fraction of nitrogen gas=
`\chi_1=(n_1)/(n_1+n_2)`

`\chi_1=(0.0428 mol)/(0.0428 mol+0.0240 mol)=0.6407\approx 0.64`

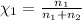
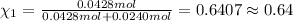
Mole fraction of oxygen gas=
`\chi_2=1-\chi_1=1-0.6407=0.3593\approx 0.36`

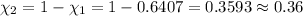
Total umber of moles in container :

n =
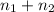`n_1+n_2`= 0.0428 mol + 0.0240 mol = 0.0668 mol

Volume of the container = V = 1.65 L

Temperature of the container = T = 15°C = 288.15 K

Total pressure in the container = P

Using an ideal gas equation:

`PV=nRT`

`P=(0.0668 mol* 0.0821 atm L/mol k* 288.15 K)/(1.65 L)`

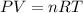
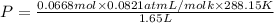
P = 0.9577 atm

Partial pressure of nitrogen gas =
`p^(o)_1`

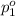
Partial pressure of nitrogen gas =
`P^(o)_2`

Partial pressure of nitrogen gas and oxygen gas can be calculated by using Dalton's law of partial pressure:

`p^(o)_i=p_(total)* \chi_i`

`p^(o)_1=P* \chi_1=0.6135 atm\approx 0.61 atm`

`p^(o)_2=P* \chi_2=0.3441 atm\approx 0.34 atm`