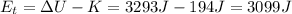Answer:
3099 J
Step-by-step explanation:
While the fireman slides down, his initial gravitational potential energy is converted partially into kinetic energy, partially into thermal energy, so we can write:
 (1)
(1)
where
![\Delta U [\tex] is the change in gravitational potential energy</p><p>K is the kinetic energy gained</p><p>Et is the thermal energy</p><p>The variation in gravitational potential energy is</p><p>[tex] U = mg \Delta h = (80 kg)(9.8 m/s^2)(4.2 m)=3293 J]()
where m=80 kg is the mass of the fireman, g=9.8 m/s^2 is the acceleration of gravity,
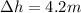 is the change in height of the fireman.
is the change in height of the fireman.
The kinetic energy gained is
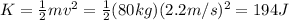
where v = 2.2 m/s is the speed reached by the fireman at the bottom of the slide
So now solving eq.(1) we find the increase in thermal energy :