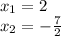Question

The function f(x)=2x^2+3x+5, when evaluated, gives a value of 19. What is the functions input value?

Answer 1

For this case we have a function of the form
`y = f (x).`

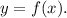
Where:

`f (x) = 2x ^ 2 + 3x + 5`

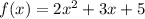
They tell us that the function has a value of 19, and we want to know the values of the input, that is:

`2x ^ 2 + 3x + 5 = 19\\2x ^ 2 + 3x + 5-19 = 0\\2x ^ 2 + 3x-14 = 0`

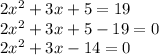
We apply the formula of the resolvent:

`a = 2\\b = 3\\c = -14`

`x = \frac {-b \pm \sqrt {b ^ 2-4 (a) (c)}} {2 (a)}\\x = \frac {-3 \pm \sqrt {3 ^ 2-4 (2) (- 14)}} {2 (2)}\\x = \frac {-3 \pm \sqrt {9 + 112}} {4}\\x = \frac {-3 \pm \sqrt {121}} {4}\\x = \frac {-3 \pm11} {4}`

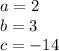
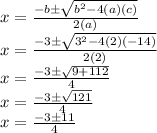
We have two roots:

`x_ {1} = \frac {-3 + 11} {4} = \frac {8} {4} = 2\\x_ {2} = \frac {-3-11} {4} = \frac {-14} {4} = - \frac {7} {2}`

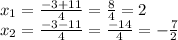
Answer:

The inputs of the function
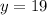`y = 19`are:

`x_ {1} = 2\\x_ {2} = - \frac {7} {2}`