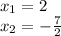For this case we have a function of the form
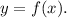
Where:
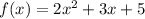
They tell us that the function has a value of 19, and we want to know the values of the input, that is:
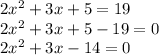
We apply the formula of the resolvent:
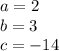
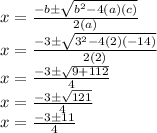
We have two roots:
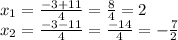
Answer:
The inputs of the function
 are:
are: