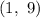Question

Find the solution of this system of equations
-6y=-50-4x
5x-6y=-49

Answer 1

1,9

Explanation:

Answer 2

`(1,\ 9)`

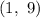
Explanation:

Rewrite the first equation

`-6y=-50-4x\\\\4x-6y=-50`

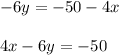
Now we have the following system of equations

`4x-6y=-50\\5x-6y=-49`

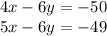
To solve the system of equations multiply the first equation by -1 and add it to the second equation

`-1*4x-(-1)*6y=-50*(-1)\\\\-4x+ 6y=50`

`-4x+ 6y=50`

+

`5x-6y=-49`

-----------------------------------

`x + 0 =1\\\\x=1`

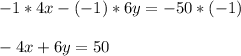
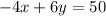
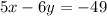
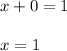
Now substitute the value of x in any of the two equations and solve for y

`5(1)-6y=-49`

`5-6y=-49`

`-6y=-49-5`

`-6y=-54`

`y=(54)/(6)`

`y=9`

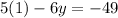
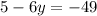
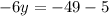
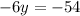
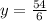
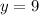
The solution is:

`(1,\ 9)`