Answer:
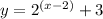
Explanation:
To solve this problem, we need to start with the parent function of the exponential function, which is
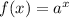 , where
, where
 is the base. In our problem,
is the base. In our problem,
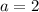 , so our parent function here is
, so our parent function here is
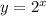 . Then, we need to perform some transformations to our parent function. Thus:
. Then, we need to perform some transformations to our parent function. Thus:
1. Vertical shrink:
A vertical shrink is a nonrigid transformation because the graph of the function get a distortion in the shape, so this transformation is as follows:
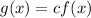
where
 in this problem equals 0.25 because:
in this problem equals 0.25 because:

2. Vertical shift:
The graph of the function
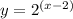 get a vertical shift given by:
get a vertical shift given by:
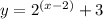
So the graph is shifted 3 units up. So the result is the graph shown above.