Question

The function relating the height of an object off the ground to the time spent falling is a quadratic relationship. Travis drops a

tennis ball from the top of an office building 90 meters tall. Three seconds later, the ball lands on the ground. After 2 seconds,
how far is the ball off the ground?
30 meters
40 meters
50 meters
60 meters

Answer 1

Answer: 50 meters

Step-by-step explanation: I just finished the pretest

Answer 2

Answer: The ball is 50 m off the ground after 2 seconds

Explanation:

Given the function relating the height of an object off the ground to the time spent falling is a quadratic relationship.

Therefore if h=height and t=time then

`h=a+bt+ct^(2)` ----------(A)

where a,b and c are constants

Apply given conditions

At t=0s h=90 m

=> 90 m = a+0+0

=>a=90 m

Also the ball has been just dropped at t=0 s

=>
`(\partial h)/(\partial t)=0=>(\partial (a+bt+ct^(2)))/(\partial t)=0`

=>
`b+2ct=0`

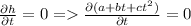
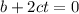
For t=0s b = 0

Thus equation (A) is reduced to
`h=90+ct^(2)`

At t= 3 s , h=0 m

`\therefore 0= 90 +9c=>c=-10 (m)/(s^(2))`

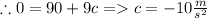
Finally we get
`h=90-10t^(2)`

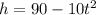
Therefore at t= 2.0 s ,
`h=(90-10* 2^(2))m=50 m`

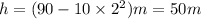
Thus the ball is 50 m off the ground after 2 seconds