Question

The revenue each season from tickets at the theme part is represented by t(x) = 3x. The cost to pay the employees each season is represented by r(x) = (1.25)x. Examine the graph of the combined function for total profit and estimate the profit after five seasons.

Answer 1

Answer: The profit after 5 seasons is $239.94.

Explanation:

Since we have given that

Revenue function is given by

`t(x)=3^x`

Cost function is given by

`r(x)=1.25^x`

So, We need to find the total profit:

As we know the formula for profit:

Profit = Revenue - Cost

`P(x)=t(x)-r(x)\\\\P(x)=3^x-1.25^x`

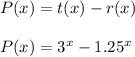
We need to evaluate the profit after five seasons:

`P(5)=3^5-1.25^5\\\\P(5)=\$239.94`

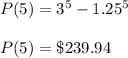
Hence, the profit after 5 seasons is $239.94.

Answer 2

240

Explanation:

Profit = revenue - cost

p(x) = 3^x - 1.25^x

5 seasons would be x = 5

p(5) = 3^5-1.25^5

p(5) = 239.948

It would be around 240