Question

F(x)= x-2/ x-4

Graph this equation and identify the points of discontinuity, holes, vertical asymptotes, x-intercepts, and horizontal asymptote.

Answer 1

The discontinuity is x = 4

There no holes

The equation of the vertical asymptote is x = 4

The x intercept is 2

The equation of the horizontal asymptote is y = 1

Explanation:

* Lets explain the problem

∵
`f(x)=(x-2)/(x-4)`

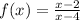
- To find the point of discontinuity put the denominator = 0 and find

the value of x

∵ The denominator is x - 4

∵ x - 4 = 0 ⇒ add 4 to both sides

∴ x = 4

* The discontinuity is x = 4

- A hole occurs when a number is both a zero of the numerator

and denominator

∵ The numerator is x - 2

∵ x - 2 = 0 ⇒ add 2 to both sides

∴ x = 2

∵ The denominator is x - 4

∵ x - 4 = 0 ⇒ add 4 to both sides

∴ x = 4

∵ There is no common number makes the numerator and denominator

equal to 0

∴ There no holes

- Vertical asymptotes are vertical lines which correspond to the zeroes

of the denominator of the function

∵ The zero of the denominator is x = 4

∴ The equation of the vertical asymptote is x = 4

- x- intercept is the values of x which make f(x) = 0, means the

intersection points between the graph and the x-axis

∵ f(x) = 0

∴
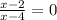`(x-2)/(x-4)=0` ⇒ by using cross multiplication

∴ x - 2 = 0 ⇒ add 2 to both sides

∴ x = 2

* The x intercept is 2

- If the highest power of the numerator = the highest power of the

denominator, then the equation of the horizontal asymptote is

y = The leading coeff. of numerator/leading coeff. of denominator

∵ The numerator is x - 2

∵ The denominator is x - 4

∵ The leading coefficient of the numerator is 1

∵ The leading coefficient of the denominator is 1

∴ y = 1/1 = 1

* The equation of the horizontal asymptote is y = 1