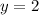Question

Which combination of integers can be used to generate the Pythagorean triple (5,12,13)

Answer 1

`x=3` and
`y=2`

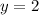
Explanation:

The Pythagorean triples can be generated by two values x, y, and a given system of equations:

`x^(2)-y^(2)=5\\2xy=12\\x^(2)+y^(2)=13`

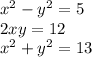
You can see that each coordinate of the triple is included in each equation.

Remember that Pythagorean triples refers to the values of each side of a right triangle, where is used the Pythagorean Theorem. But, at a higher level, to construct this triples we use the system of equations, with two integers x and y., like this case.

Now we solve the system, the best first step is to just sum the first and third equations, because they have like terms:

`2x^(2)=18\\x^(2)=(18)/(2)=9\\x=3`

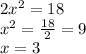
Now, we just replace it in the second equation:

`2xy=12\\y=(12)/(2x)=(6)/(3)=2`

Therefore the integers that generate the Pythagorean triple
`(5,12,13)` are
`x=3` and
`y=2`

Answer 2

x=3 and y=2

Explanation:

The pythagorean triples are generated by two integrers x and y that can be found by solving the following system of equations:

`\left \{ {{x^(2)-y^(2)=5}\atop {2xy=12}} \atop {x^(2)+y^(2)=13}}\right.`

Solve the system of equations, and we get that the solution is x=3 and y=2.

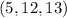Therefore, the combination of integrers that ca be used to generate the pythagorea triple are: x=3 and y=2