Question

The hypotenuse of right triangle ABC, line segment AC, measures 13 cm. The length of line segment BC is 5 cm.

What is the approximate difference between m∠C and m∠A?

Answer 1

The approximate difference between m∠C and m∠A is 45° to the nearest degree

Explanation:

* Lets talk about the right triangle

- It has one right angle and two acute angles

- The side opposite the the right angle is called hypotenuse

- The other sides are called the legs of the right angle

- In ΔABC

∵ AC is the hypotenuse

∴ ∠B is the right angle

∴ AB and BC are the legs of the right angle

∴ Angles A and C are the acute angles

∵ m∠B = 90°

- The sum of the measures of the interior angles of a Δ is 180°

∴ m∠A + m∠C = 180° - 90° = 90°

- We will use trigonometry to find the measures of angles A and C

- sin A is the ratio between the opposite side to angle ∠A and the

hypotenuse

∵ BC is the opposite side of angle A

∴ sin A = BC/AC

∵ BC = 5 cm

∵ AC = 13 cm

∴ sin A = 5/13

- Lets find m∠∠A by using sin ^-1

∴ m∠A =
`sin^(-1)(5)/(13)=22.62`

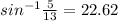
- Lets use the rule of the sum of angles A and C to find the measure

of the angle C

∵ m∠A + m∠C = 90°

∴ 22.62° + m∠C = 90 ⇒ subtract 22.62 from both sides

∴ m∠C = 67.38°

- Lets find the difference between m∠C and m∠A

∴ The approximate difference between m∠C and m∠A is:

67.38° - 22.62° = 44.78° ≅ 45° to the nearest degree