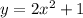Answer:
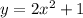
Explanation:
we know that
The graph is a vertical parabola open upward
The vertex is the point (0,1)
The equation of a vertical parabola in vertex form is equal to
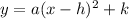
substitute the vertex in the equation
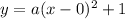
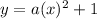
Find the value of coefficient a
Observing the graph
For x=1, y=3
substitute in the equation
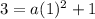
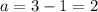
The equation on the graph is equal to