2 Answers

Bep · Answer 1 · 2020-03-28T06:45:36+0000

Answer:

90°

Explanation:

First you must calculate the module or the magnitude of both vectors

The module of u is:

$|u|=√((8)^2 + (-3)^2) \\\\|u|=√(64 + 9)\\\\|u|=8.544$

The module of v is:

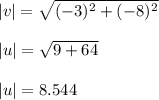
$|v|=√((-3)^2 + (-8)^2) \\\\|u|=√(9 + 64)\\\\|u|=8.544$

Now we calculate the scalar product between both vectors

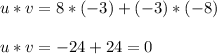
$u*v = 8*(-3) + (-3)*(-8)\\\\u*v = -24+ 24=0$

Finally we know that the scalar product of two vectors is equal to:

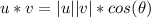
$u*v = |u||v|*cos(\theta)$

Where
$\theta$ is the angle between the vectors u and v. Now we solve the equation for
$\theta$

$0 = 8.544*8.544*cos(\theta)\\\\0 = cos(\theta)\\\\\theta= arcos(0)\\\\\theta=90\°$

the answer is 90°

Whenever the scalar product of two vectors is equals to zero it means that the angle between them is 90 °