Question

A charge partides round a 1 m radius circular particle accelerator at nearly the speed of light. Find : (a) The period (b) The centripetal acceleration of the charged particles

Answer 1

Step-by-step explanation:

It is given that,

Radius of circular particle accelerator, r = 1 m

The distance covered by the particle is equal to the circumference of the circular path, d = 2πr

d = 2π × 1 m

(a) The speed of satellite is given by total distance divided by total time taken as :

`speed=(distance)/(time)`

Let t is the period of the particle.

`t=(d)/(s)`

d = distance covered

s = speed of particle

It is given that the charged particle is moving nearly with the speed of light

`t=(d)/(c)`

`t=(2\pi* 1\ m)/(3* 10^8\ m/s)`

`t=2.09* 10^(-8)\ s`

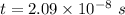
(b) On the circular path, the centripetal acceleration is given by :

`a=(c^2)/(r)`

`a=((3* 10^8\ m/s)^2)/(1\ m)`

`a=9* 10^(16)\ m/s^2`

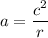
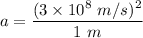
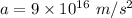
Hence, this is the required solution.