Question

When the pressure that a gas exerts

on a sealed container changes from
22.5 psi to_ psi, the
temperature changes from 110°C to
65.9°C.

Answer 1

The final pressure at 65.9°C is 19.91 psi.

Step-by-step explanation:

To calculate the final pressure of the system, we use the equation given by Gay-Lussac Law.

This law states that pressure of the gas is directly proportional to the temperature of the gas at constant pressure.

Mathematically,

`(P_1)/(T_1)=(P_2)/(T_2)` (at constant Volume)

where,

`P_1\text{ and }T_1` are the initial pressure and temperature of the gas.

`P_2\text{ and }T_2` are the final pressure and temperature of the gas.

We are given:

`P_1=22.5 psi\\T_1=110^oC=383.15 K\\P_2=?\\T_2=65.9^oC=339.05 K`

Putting values in above equation, we get:

`(22.5 psi)/(383.15 K)=(p_2)/(339.05 K)`

`P_2=(22.5 psi)/(383.15 K)* 339.05 K=19.91 psi`

The final pressure at 65.9°C is 19.91 psi.

Answer 2

Hello!

The answer is:

When the pressure that a gas exerts on a sealed container changes from

22.5 psi to 19.86 psi, the temperature changes from 110°C to

65.9°C.

Why?

To calculate which is the last pressure, we need to use Gay-Lussac's law.

The Gay-Lussac's Law states that when the volume is kept constant, the temperature (absolute temperature) and the pressure are proportional.

The Gay-Lussac's equation states that:

`(P_1)/(T_1)=(P_2)/(T_2)`

We are given the following information:

We need to remember that since the temperatures are given in Celsius degrees, we need to convert it to Kelvin (absolute temperature) before use the equation, so:

`P_1=22.5Psi\\T_1=110\°C=110\°C+273.15=383.15K\\T_1=65.9\°C=65\°C+273.15=338.15K`

Now, calculating we have:

`(P_1)/(T_1)*(T_2)=P_2\\\\P_2=(P_1)/(T_1)*(T_2)=(22.5Psi)/(383.15)*338.15=19.86Psi`

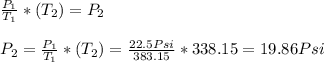
Hence, the final pressure is equal to 19.86 Psi.

Have a nice day!