Answer:
The correct answer is option D.
Step-by-step explanation:
Formula used for the radius of the
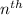 orbit will be,
orbit will be,
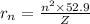 (in pm)
(in pm)
where,
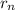 = radius of
= radius of
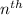 orbit
orbit
n = number of orbit
Z = atomic number
Radius of the first orbit, n = 1
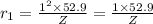 ..[1]
..[1]
Radius of the third orbit, n = 3
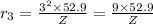 ..[2]
..[2]
[1] ÷ [2]


The radius of the 3rd orbit is nine times the radius of first orbit.