Question

Consider the paragraph proof.

Given: D is the midpoint of AB, and E is the midpoint of AC.
Prove:DE = BC



It is given that D is the midpoint of AB and E is the midpoint of AC. To prove that DE is half the length of BC, the distance formula, d = , can be used to determine the lengths of the two segments. The length of BC can be determined with the equation BC = , which simplifies to 2a. The length of DE can be determined with the equation DE = , which simplifies to ________. Therefore, BC is twice DE, and DE is half BC.

Which is the missing information in the proof?

a
4a
a2
4a2

Answer 1

a

Explanation:

You're trying to find the distance between D and E so u use the distance formula.

sqrt (a+b-b^2)+(c-c)^2=sqrt a^2=a

Answer 2

a

Explanation:

We are given that

D is the mid-point of AB and E is the mid-point of AC.

We have to find the missing information in given proof of DE is equal to half of BC.

Proof:

D is the mid-point of AB and E is the mid-point of AC.

The coordinates of A are (2b,2c)

The coordinates of D are (b,c)

The coordinates of E are (a+b,c)

The coordinates of B are (0,0)

The coordinates of C are (2a,0)

Distance formula:
`√((x_2-x_1)^2+(y_2-y_1)^2)`

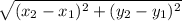
Using the formula

Length of BC=
`√((2a)^2+(0-0)^2)=2a` units

Length of DE=
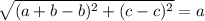`√((a+b-b)^2+(c-c)^2)=a` units

`BC=2a=2* DE`

`DE=(1)/(2)BC`

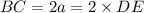
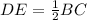
Hence, proved.

Option A is true.