Question

Helppp please thanks so much!

Answer 1

I'll assume this is:

Show

`(\sin 2a + \cos 2a)/(2 \cos a + \sin a - 2(\cos ^3 a + \sin ^3 a)) = \csc a`

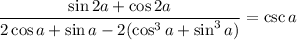
What a mess. Who comes up with these?

Somehow the whole thing has to factor so the numerator and denominator cancel and we're left with sin a in the denominator.

We have the sum of cubes so we'll probably need to know the factorization

`x^3 + y^3 = (x + y) (x^2 - x y + y^2)`

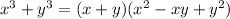
Let's just start with the denominator and factor this way.

`2 \cos a + \sin a - 2(\cos ^3 a + \sin ^3 a)`

`= 2 \cos a + \sin a - 2(\cos a + \sin a)(\cos^2 a - \cos a \sin a + \sin ^2 a)`

`= 2 \cos a + \sin a - 2(\cos a + \sin a)(1 - \cos a \sin a)`

`= 2 \cos a + \sin a - 2\cos a-2 \sin a +2(\cos a + \sin a)\cos a \sin a`

`= -\sin a +2(\cos a + \sin a)\cos a \sin a`

`= \sin a (-1 + 2 \cos a(\cos a + \sin a))`

`= \sin a(2 \cos^2 a - 1 + 2 \sin a \cos a)`

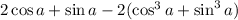
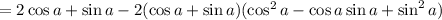
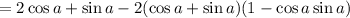
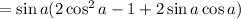
We recognize the double angle formulas,

`= \sin a(\cos 2a + \sin 2a)`

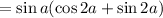
So

`(\sin 2a + \cos 2a)/(2 \cos a + \sin a - 2(\cos ^3 a + \sin ^3 a))`

`=(\sin 2a + \cos 2a)/( \sin a(\cos 2a + \sin 2a))`

`=(1)/(\sin a)`

`=\csc a \quad\checkmark`

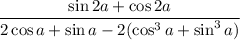
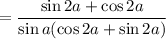
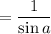
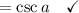
Phew.