Question

find the slope intercept form for the equation of a line which passes through the point( 7, 4) and the origin​

Answer 1

y =
`(4)/(7)`x

Step-by-step explanation:

Slope-intercept form is y = mx + b

m is the slope (rise over run)

b is the y-intercept (where the line crosses the y-axis)

To get the slope, use the formula
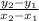`(y_(2) - y_(1) )/(x_(2) - x_(1))`. It doesn't matter which set of coordinates is which pair.

(x₁,y₁) = (7,4)

(x₂,y₂) = (0,0) a.k.a "the origin"

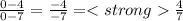`(0-4)/(0-7) = (-4)/(-7) = <strong>(4)/(7)` = your slope (m)

Now, to get to slope-intercept form, you have to plug what you know into point-slope form, y - y₁ = m(x - x₁).

y₁ = a point on the line

m = slope

x₁ = the matching coordinate to y₁

y - 4 =
`(4)/(7)` (x - 7) Distribute

y - 4 =
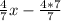`(4)/(7) x - (4*7)/(7)` Simplify

y - 4 =
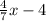`(4)/(7)x - 4` Add 4 to both sides

y =
`(4)/(7)`x + 0 or y =
`(4)/(7)`x

Check your work by plugging in your given coordinates:

y =
`(4)/(7)`x

0 =
`(4)/(7)`(0)

0 = 0

and

y =
`(4)/(7)`x

4 =
`(4)/(7)`(7)

4 =
`(4*7)/(7)`

4 = 4