Question

For waht values of x do the vectors -1,0,-1), (2,1,2), (1,1, x) form a basis for R3?

Answer 1

The values of x for which the given vectors are basis for R³ is:

`x\\eq 1`

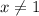
Explanation:

We know that for a set of vectors are linearly independent if the matrix formed by these set of vectors is non-singular i.e. the determinant of the matrix formed by these vectors is non-zero.

We are given three vectors as:

(-1,0,-1), (2,1,2), (1,1, x)

The matrix formed by these vectors is:

`\left[\begin{array}{ccc}-1&2&1\\0&1&1\\-1&2&x\end{array}\right]`

Now, the determinant of this matrix is:

`\begin{vmatrix}-1 &2 & 1\\ 0& 1 & 1\\ -1 & 2 & x\end{vmatrix}=-1(x-2)-2(1)+1\\\\\\\begin{vmatrix}-1 &2 & 1\\ 0& 1 & 1\\ -1 & 2 & x\end{vmatrix}=-x+2-2+1\\\\\\\begin{vmatrix}-1 &2 & 1\\ 0& 1 & 1\\ -1 & 2 & x\end{vmatrix}=-x+1`

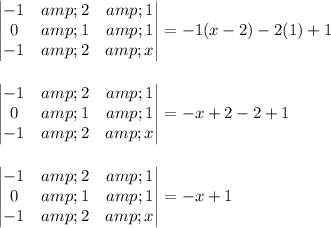
Hence,

`-x+1\\eq 0\\\\\\i.e.\\\\\\x\\eq 1`