Question

An arrow is shot vertically upward at a rate of 180ft/s. Use the projectile formula h=?16t2+v0t to determine at what time(s), in seconds, the arrow is at a height of 420ft. Round your answer(s) to the nearest tenth of a second.

Answer 1

Hello!

The answer is:

`t_1=3.60s\\t_2=7.94s`

Time equal to 3.30 seconds when the arrow was going up.

Time time equal to 7.94 seconds when the arrow was going down.

Why?

To solve the problem, we need to solve the quadratic equation and find the value of values of time where the height of the arrow is 420 feet.

Also, we are given some information, we need to substitute it and then use the quadratic equation.

The equation is:

`h=-16t^(2)+vot\\\\-16t^(2)+vot-h=0`

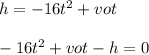
Substituting the given information we have:

`-16t^(2)+vot-h=0`

`-16t^(2)+180(ft)/(s) t-420=0`

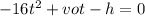
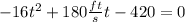
We have a quadratic equation where:

`a=-16\\b=180\\c=-420`

Now, using the quadratic equation to find the value or values of "t", we have:

`\frac{-b+-\sqrt{b^(2)-4ac } }{2a}`

`\frac{-180+-\sqrt{180^(2)-4*-16*-420 } }{2*-16}=(-180+-√(32400-26880 ) )/(-32)\\\\(-180+-√(32400-26880))/(-32)=(-180+-√(5520))/(-32) \\\\(-180+-√(5520))/(-32)=(-180+-(74.29))/(-32)\\\\t_1=(-180+(74.29))/(-32)=3.30\\\\t_2=(-180-(74.29))/(-32)=7.94`

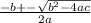
Hence, we have two positive values of time, it means that there are two moments of time where the height of the arrow is equal to 420 feet, those times are:

`t_1=3.60s\\t_2=7.94s`

Time equal to 3.30 seconds when the arrow was going up.

Time equal to 7.94 seconds when the arrow was going down.

Have a nice day!

Answer 2

3.3secs, 7.9secs

Explanation:

We are looking for the number of seconds it takes the arrow to reach a height of 420ft. We are given the projectile formula h=−16t2+v0t, where h is the height, in feet, and t is the time, in seconds. We can substitute the initial velocity v0=180 and desired height h=420 to find

420=−16t2+180t

Rewriting this quadratic equation in standard form, we have

16t2−180t+420=0

Now that the equation is in standard form, at2+bt+c=0, we can identify the coefficients a=16, b=−180, and c=420. Substituting these into the quadratic formula, we have

t=−b±b2−4ac‾‾‾‾‾‾‾‾√2a=−(−180)±(−180)2−4(16)(420)‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√2(16)=180±5520‾‾‾‾‾√32

The approximate values for t are

t=≈180+5520‾‾‾‾‾√327.9andt=≈180−5520‾‾‾‾‾√323.3

The arrow will go up and then fall down. As the arrow goes up, it will reach 420ft after approximately 3.3s. It will also pass that height on the way down at approximately 7.9s.