Question

Consider the following matrix A={{1,-1,0,0},{2,-1,0,0},{0,0,1,0},{-1,-1,0,1}}Which of the following statements is true? Check the correct answer(s) below.A. The homogeneous system Ax=0 has infinitely many solutionsB. The matrix A has determinant −1C. The matrix A is not invertibleD. The matrix A is singular.E. None of the above

Answer 1

The correct answer is:

Option: E

E. None of the above

Explanation:

• We know that a system of equation i.e.

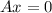`Ax=0` has infinite many solutions if det(A)=0

• Also, the matrix is singular if det(A)=0

and is non-singular or invertible otherwise i.e. when det(A)≠0

• We know that when a homogeneous system has i.e.
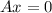  `Ax=0` is such that: |A|≠0 then the system has a unique solution.

The matrix that will be formed by the given set of vectors is:

`A=\begin{bmatrix}-1 &2 &0 &-1 \\ -1&-1 &0 &-1 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1 \end{bmatrix}`

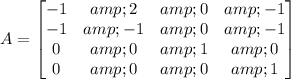
Also, determinant i.e. det of matrix A is calculated by:

`\begin{vmatrix}-1 &-2 &0 &-1 \\ -1&-1 &0 &-1 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1 \end{vmatrix}=1(1(1+2))=3`

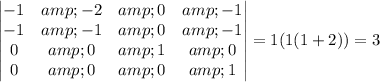
Hence, determinant is not equal to zero.

This means that the matrix is invertible and non-singular.