Question

Points A and B have coordinates (3,1,2) and (1,-5,4) respectively. Point C lies on line AB such that AC:BC=3:2. Find position vector of Point C.

Final answer is (-3,-17,8)

Answer 1

The position vector of point C is <-3 , -17 , 8> or -3i - 17j + 8k

Explanation:

* Lets revise how to solve the problem

- If the endpoints of a segment are (x1 , y1 , z1) and (x2 , y2 , z2), and

point (x , y , z) divides the segment externally at ratio m1 :m2, then

`x=(m_(1)x_(2)-m_(2)x_(1))/(m_(1) -m_(2)),y=(m_(1)y_(2)-m_(2)y_(1))/(m_(1)-m_(2)),z=(m_(1)z_(2)-m_(2)z_(1))/(m_(1)-m_(2))`

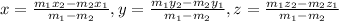
* Lets solve the problem

∵ AB is a segment where A = (3 , 1 , 2) and B = (1 , - 5 , 4)

∵ Point C lies on line AB such that AC : BC=3 : 2

∵ From the ratio AC = 3/2 AB

∴ C divides AB externally

- Lets use the rule above to find the coordinates of C

- Let Point A is (x1 , y1 , z1) , point B is (x2 , y2 , z2) and point C is (x , y , z)

and AC : AB is m1 : m2

∴ x1 = 3 , x2 = 1

∴ y1 = 1 , y2 = -5

∴ z1 = 2 , z2 = 4

∴ m1 = 3 , m2 = 2

- By using the rule above

∴
`x=(3(1)-2(3))/(3-2)=(3-6)/(1)=(-3)/(1)=-3`

∴
`y=(3(-5)-2(1))/(3-2)=(x=-15-2)/(1)=(-17)/(1)=-17`

∴
`z=(3(4)-2(2))/(3-2)=(12-4)/(1)=(8)/(1)=8`

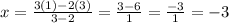
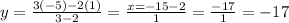
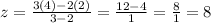
∴ The coordinates fo point c are (-3 , -17 , 8)

* The position vector of point C is <-3 , -17 , 8> or -3i - 17j + 8k