Question

Which formula can be used to determine the total number of different eight-letter arrangements that can be formed using the letters in the word "CLIMBING"?

Answer 1

The word "climbing" has 8 letters, so there are
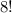`8!` permutations of all the letters.

Nevertheless, the letters are not unique: there are 2 I's. This means that, if we start from a given word and we exchange the positions of the two I's, we'd still get the same word. So, we have to divide the number of possible permutations by
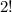`2!`, because for any given permutation there are two identical words, given by the interchange of the I's.

So, the number of possible words is

`(8!)/(2!) = (8*7*6*5*4*3*2)/(2)=8*7*6*5*4*3=40320`