Question

When a factor x − k is raised to an odd power, the graph crosses the x-axis at x = k.

When a factor x − k is raised to an even power, the graph only touches the x-axis at x = k.

Describe the graph of the function g(x) = (x − 1)(x + 4)3(x + 5)2. 
The graph: 
crossesdoes not intersecttouches the axis at (1, 0). 
crossesdoes not intersecttouches the axis at (−4, 0). 
crossesdoes not intersecttouches the axis at (−5, 0)

​

Answer 1

crosses at (1,0)

crosses at (-4,0)

touches at (-5,0)

Got correct on ed

Explanation:

Answer 2

The graph of
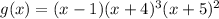`g(x) = (x - 1) (x + 4)^3(x +5)^2` crosses the x-axis at (1,0) and (-4, 0). It touches the x-axis at (-5, 0).

Explanation:

g(x):

`g(x) = (x - 1) (x - (-4))^3(x - (-5)^2`.

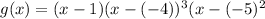There are three factors:

• (x - 1), where k = 1,
• (x - (-4)), where k = -4, and
• (x - (-5)), where k = -5.

The first and second factors are raised to odd powers. The graph will cross the x-axis at all these two points:

• (1, 0) as a result of the factor (x - 1),
• (-4, 0) as a result of the factor (x - (-4)).

The third factor is raised to an even power. The graph will touch the x-axis at that point.

• (-5, 0) as a result of the factor (x - (-5)).