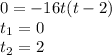Question

Gianna is going to throw a ball from the top floor of her middle school. When she throws the ball from 48feet above the ground, the function h(t)=−16t2+32t+48 models the height, h, of the ball above the ground as a function of time, t. Find the times the ball will be 48feet above the ground.

Answer 1

`\bf \stackrel{height}{h(t)}=-16t^2+32t+48\implies \stackrel{48~ft}{~~\begin{matrix} 48 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}=-16t^2+32t~~\begin{matrix} +48 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix} \\\\\\ 0=-16t^2+32t\implies 16t^2-32t=0\implies 16t(t-2)=0\implies t= \begin{cases} 0\\ 2 \end{cases}`

t = 0 seconds, when the ball first took off, and t = 2, 2 seconds later.

Answer 2

Answer:
`t_1=0\\t_2=2`

Explanation:

We know that the function
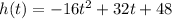`h(t)=-16t^2+32t+48` models the height "h" of the ball above the ground as a function of time "t".

Then, to find the times in which the ball will be 48 feet above the ground, we need to substitute
`h=48` into the function and solve fot "t":

`48=-16t^2+32t+48\\0=-16t^2+32t+48-48\\0=-16t^2+32t`

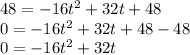
Factorizing, we get:

`0=-16t(t-2)\\t_1=0\\t_2=2`