Answer:
P(A given B) = 3/4
Explanation:
As we know that it is conditional probability, where the probability of an event depends on the event that has certain probability of occurrence.
The formula for conditional probability is:
P(A given B) = P(A ∩B) / P(B)
Where a and B are events. The probability of event B is known and we also know probability of A∩B
So, putting the values in the formula:
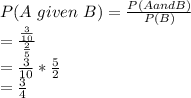
So, the probability of A given B is 3/4 ..