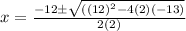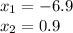Answer:
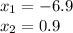
Explanation:
The first step is to move all the terms from the right side to the left side of the equation and then add the like terms:
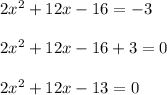
Now we can apply the Quadratic formula. This is:
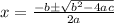
In this case we can identify that:
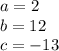
Finally, we must substitute these values into the Quadratic formula. Then we get: