Question

A family has two cars. The first car has a fuel efficiency of 20 miles per gallon of gas and the second has a fuel efficiency of 35 miles per gallon of gas. During one particular week, the two cars went a combined total of 1225 miles, for a total gas consumption of 50 gallons. How many gallons were consumed by each of the two cars that week?

first car:
Second:

Answer 1

First car: 35 gallons

Second car: 15 gallons

Explanation:

Set up a system of equations.Let be "x" the number of gallons consumed by the first car and "y" the number of gallons consumed by the second car.

Then:

`\left \{ {{x+y=50} \atop {20x+35y=1,225}} \right.`

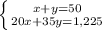
Applying the Elimination method, multiply the first equation by -20, then add both equations and solve for "y":

`\left \{ {{-20x-20y=1,000} \atop {20x+35y=1,225}} \right. \\.......................\\15y=225\\y=15`

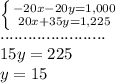
Substitute this value into the first equation and solve for "x":

`x+15=50\\x=35`

Answer 2

First car: 35 gallons

Second car: 15 gallons

Explanation:

Assuming
`x` to be the gas consumed by 1st car and
`50 - x` to be the gas consumed by 2nd car.

We know that:

Distance traveled = fuel efficiency × gas consumed

`20x+35(50-x)=1225`

`20x+1750-35x=1225`

`35x-20x=1750-1225`

`15x=525`

`x=35`

So
`50 - x = 50-35=15`

Therefore, first car consumed 35 gallons while second car consumed 15 gallons.