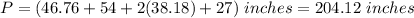Answer: 204.12 inches
Explanation:
We can find the lengths of the unknown sides by applying these identities:
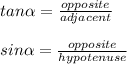
Observe the image attached. To find "a" we need to substitute the following values into
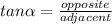 :
:
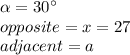
And solve for "a":
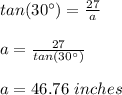
To find "b" we need to substitute the following values into
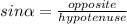 :
:
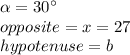
And solve for "b":
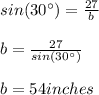
To find "c" we need to substitute the following values into
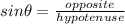 :
:
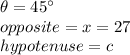
And solve for "c":
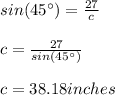
Since the triangle on the left is Isosceles, then:
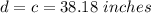
Therefore, the perimeter is: