Question

Which expression is equivalent to (x^4/3 x^2/3)^1/3?

Answer 1

B

Explanation:

Just took the test

Answer 2

Answer:
`x^{(2)/(3) }`

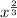
Explanation:

We have several properties of exponents in use here. The two that are used are:

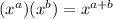`(x^(a))(x^(b)) = x^(a + b)` (Exponents with the same base that are being multiplied together can have the exponents added)

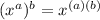`(x^(a))^(b) = x^((a)(b))` (A base raised to a power, and then raised to another power means that you can multiply the exponents to get the same result as doing inside operations and then outside operations)

Let's apply it!

First, let's simplify what's inside the parenthesis.

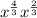`x^{(4)/(3) } x^{(2)/(3) }` (Remember, they have the same base of "x", so we can add the exponents)

`x^{(4)/(3) + (2)/(3) }` =
`x^{(6)/(3) }` =
`x^(2)`

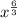Now we have
`(x^(2))^{(1)/(3) }`. Let's use the second rule.

`(x^(2))^{(1)/(3) }` =
`x^{(2)/(3) }`

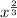
Hope this helps! :^)