Start with 2 arbitrary vectors,
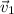 and
and
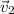 . (pic 1)
. (pic 1)
Vectors are determined by their lengths and direction. This means that translating the vector (i.e. sliding it left/right and up/down in the plane) doesn't fundamentally change that vector. To this end, we could just as easily represent
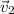 as if it had originated from the tip of
as if it had originated from the tip of
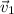 . This "new"
. This "new"
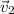 and the "old"
and the "old"
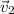 are the same vector. (pic 2)
are the same vector. (pic 2)
If we connect the origin of
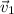 with the tip of "new"
with the tip of "new"
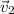 , we get a new vector, and this we define as the vector sum
, we get a new vector, and this we define as the vector sum
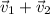 . (pic 3)
. (pic 3)
We can do this other way, by first traslating
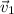 to the tip of
to the tip of
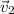 , then connecting the origin of
, then connecting the origin of
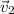 with the tip of "new"
with the tip of "new"
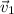 . This demonstrates that vector addition is commutative (order of the vectors being added doesn't matter - you always end up at the same terminus). The "parallelogram method" refers to how a parallelogram is traced out. (pic 4)
. This demonstrates that vector addition is commutative (order of the vectors being added doesn't matter - you always end up at the same terminus). The "parallelogram method" refers to how a parallelogram is traced out. (pic 4)
Multiplying a vector by -1 reverses its direction. (pic 5)
Adding
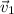 and
and
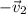 works the same way as standard vector addition, giving us the new vector
works the same way as standard vector addition, giving us the new vector
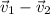 . (pic 6)
. (pic 6)
We can do the same in the reverse order, but now we get a different vector,
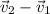 . (pic 7)
. (pic 7)
These vectors have the same length but point in opposite directions. (pic 8)
But notice that we can translate the vectors
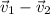 and
and
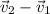 so that we get a vector that either starts at the tip of
so that we get a vector that either starts at the tip of
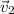 and ends at the tip of
and ends at the tip of
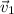 (pic 9), or starts at the tip of
(pic 9), or starts at the tip of
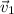 and ends at the tip of
and ends at the tip of
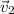 (pic 10). The "triangle method" refers to the triangles that are traced out by either vector sum
(pic 10). The "triangle method" refers to the triangles that are traced out by either vector sum
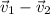 and
and
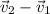 together with
together with
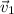 and
and
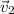 .
.