For this case we must factor the following expression:
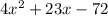
We rewrite the middle term as a sum of two terms whose product is
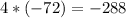 and whose sum is 23. These numbers are -9 and +32. So:
and whose sum is 23. These numbers are -9 and +32. So:
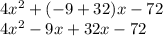
We factor the highest common denominator of each group.
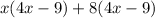
We factor taking into account the common term
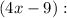
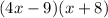
Finally, the factored expression is:
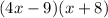
Answer:
Option D