Answer: Option B
Explanation:
By definition, only those functions that are one to one have an inverse function.
A function is one by one if there are not two different input values,
 and
and
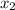 , that have the same output value y
, that have the same output value y
Note that the function
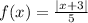 is not a one-to-one function
is not a one-to-one function
When x=2
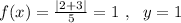
When x=8
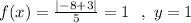
Note that the function
 is not a one-to-one function
is not a one-to-one function
When x=1

When x=-1

Note that the function
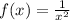 is not a one-to-one function
is not a one-to-one function
When x=1
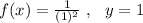
When x=-1
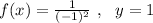
Then the answer is the option B.
You can verify that The function
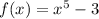 is a one-to-one function and therefore its inverse is a function
is a one-to-one function and therefore its inverse is a function