Question

Which of the following is missing in the explicit formula for the compound interest geometric sequence below?

Answer 1

1+i

Explanation:

The explicit formula for the compound interest geometric tell us: If P1 is invested at an interest rate of i per year, compounded annually, the future value Pn at the end of the nth year is:

`Pn=P1(1+i)^((n-1))`

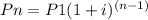
For example if you have $10 at 5% at an interest rate of 5% per year.

Then if you want to know the amount of money at the end of the 2, 3 and 4 year, you have:

n=1 year P1=10

n=2 year

`P2=10(1+(5/100))`

`P2=10(1+(5/100))^((2-1))`

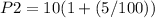
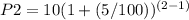
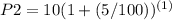`P2=10(1+(5/100))^((1))`=10,5

n=3 year

`P3=10(1+(5/100))*(1+(5/100))`

`P3=10(1+(5/100))^((3-1))`

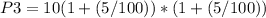
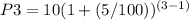
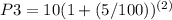`P3=10(1+(5/100))^((2))`=11.025

n=4 year

`P4=10(1+(5/100))*(1+(5/100))*(1+(5/100))`

`P4=10(1+(5/100))^((4-1))`

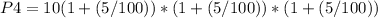
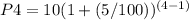
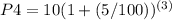`P4=10(1+(5/100))^((3))`= 11.57625